L’algorithme de base

L’algorithme régissant le jeu de la vie en 3D se rapproche grandement de l’algorithme 2d. Cependant, ils différents par le nombre de cases à vérifier à chaque itérations. L’ajout d’une dimension entraine la vérification de 26 cases au lieu de 8.

Pour des tests sur les réponses de l’algorithme, j’ai décidé d’ajouter la possibilité de modifier les conditions de vie et de mort des cellules.

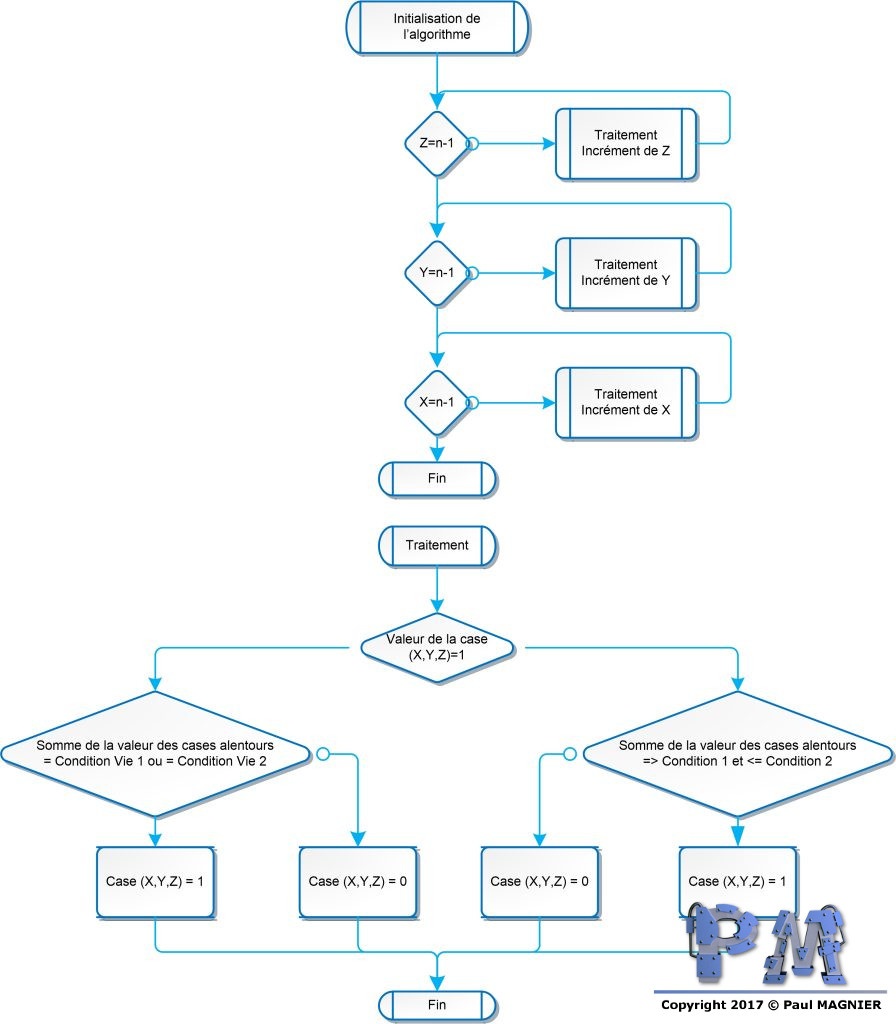
1. Lors de l’initialisation, l’algorithme copie la grille pour avoir une base de comparaison. La grille copiée servira à la vérification de la valeur des cases et la grille de base sera modifiée par l’algorithme.
2. L’algorithme vérifie ensuite le tableau case par case
   1. Puis il additionne la valeur des 26 cases avoisinantes si celle-ci existent.
   2. Si la valeur de la case est 1
      1. La cellule ne peut survivre qu’à la condition d’avoir entre Condition 1 et Condition 2 voisines vivantes.
   3. Si la valeur de la case est 0
      1. La cellule morte renait si elle possède exactement Condition vie 1 ou Condition vie 2 voisines vivantes.

La recherche des invariances

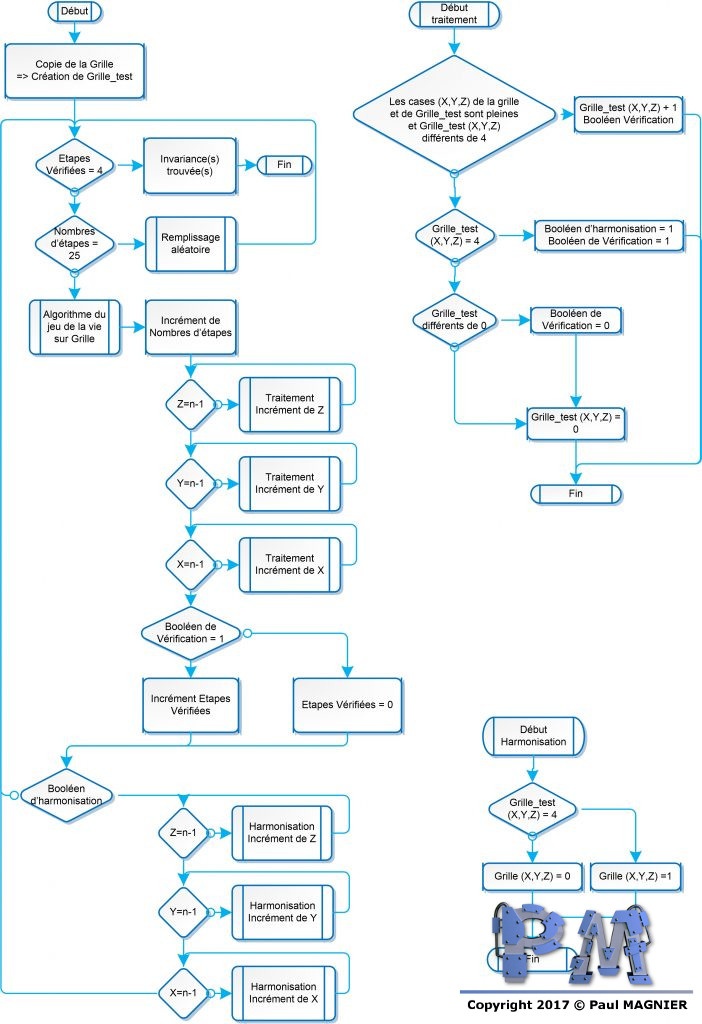
La recherche d’invariance de manière manuelle étant longue et fastidieuse, j’ai décidé d’automatiser le processus à l’aide de l’algorithme suivant :

1. Copie de la Grille de base. On appellera la grille copié Grille_Test.
2. Passage dans l’algorithme du jeu de la vie de la Grille de base.
3. L’algorithme compare ensuite les deux grilles
   1. Si la case (x,y,z) est pleine dans les deux grilles,
      1. alors si la valeur de la case de Grille_Test est inférieure à 4, on incrémente celle-ci.
      2. sinon, on lance l’harmonisation.
   2. Si les cases sont différentes, alors la valeur de la case est mise à 0.
4. Si une des cases de Grille_Test à pour valeur 4, on lance l’harmonisation, c’est à dire que les seules cases pleines dans la Grille seront celles ayant pour valeur 4 dans la Grille_Test.
5. Si les cases des deux grilles sont identiques, on incrémente le nombre d’étapes vérifiées. Il est remis à zéro à partir du moment où une différence est enregistrée.
6. Si le nombre d’étapes vérifiées atteint 4, l’algorithme à trouvée une invariance. Sinon, si cette algorithme à été exécuté 25 fois, alors, on lance le remplissage aléatoire et on recommence.

Pourquoi avoir choisi 4 pour valeur de test dans le dernier algorithme?

1. L’algorithme test si les cases de la grille change ou pas. Si la valeur d’une case de la grille test est 4, cela signifie que cette case de la grille n’a pas été modifiée pendant 4 étapes. La valeur 1 n’était pas possible, celle-ci correspondant à la valeur d’une case pleine. Il n’est pas rare qu’une case ne change pas d’état durant 2-3-4-5-6 étapes. Alors pourquoi quatre? Les valeurs deux et trois m’ont parus trop faible pour être significative d’une invariance. Comme on recherche des invariances, des valeurs plus élevées semblerait préférable mais le risque que la figure d’invariance soit polluée par l’extension des autres figures, et donc disparaisse, deviens de plus en plus important. La valeur quatre m’as donc parût être un bon compromis d’après les différents tests que j’ai effectué.
2. Après avoir vérifié quatre fois qu’une partie de la grille ne changeait pas, on isole cette partie en mettant toutes les cases ayant une valeur différente de 4 à 0. On refait ensuite passer cette « nouvelle grille » dans l’algorithme pour vérifier si elle est invariante ou non. Les cases qui ne forment pas une figure d’invariance seront modifiées dès la première étape et donc la valeur vérification restera à zéro. La valeur quatre permet de s’assurer que la figure est bien une figure d’invariance même si une valeur de trois aurait pus fonctionner (pour plus de sureté, j’ai éliminé d’office la valeur 2).