Introduction

Le jeu de la vie est un automate fini particulier proposé par John Conway de Cambridge dans les années 1970.

Un automate fini est une machine réalisant une seule action à partir d’une donnée d’entrée en respectant des règles prédéfinies.

Le jeu se déroule sur une grille à deux dimensions, théoriquement infinie (mais de longueur et de largeur finies et plus ou moins grandes dans la pratique. Les cases, qu’on appelle des « cellules », par analogie avec les cellules vivantes, peuvent prendre deux états distincts : « vivantes » ou « mortes ».

À chaque étape, l’évolution d’une cellule est entièrement déterminée par l’état de ses huit voisines de la façon suivante :

• Si à un instant t une case est occupée par une particule, et qu’elle possède plus de trois voisins, alors à l’instant t+1 la particule meurt.
• Si à un instant t une case est occupé par une particule, et qu’elle possède moins de deux voisins, alors à l’instant t+1 la particule meurt.
• Si à un instant t une case est vide, et qu’elle possède exactement 3 voisins, alors à l’instant t+1 une nouvelle particule nait dans cette case.

Une cellule ne peut donc survivre qu’à la condition d’avoir 2 ou 3 voisins.

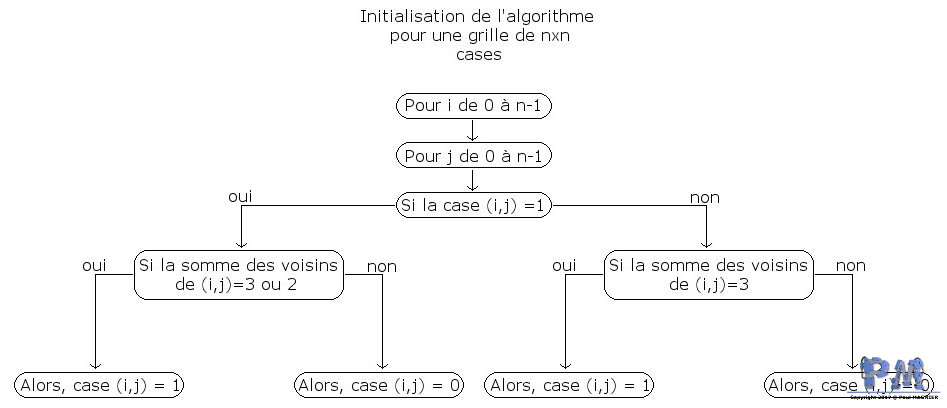
Logigramme

La transcription logique de cet algorithme est :

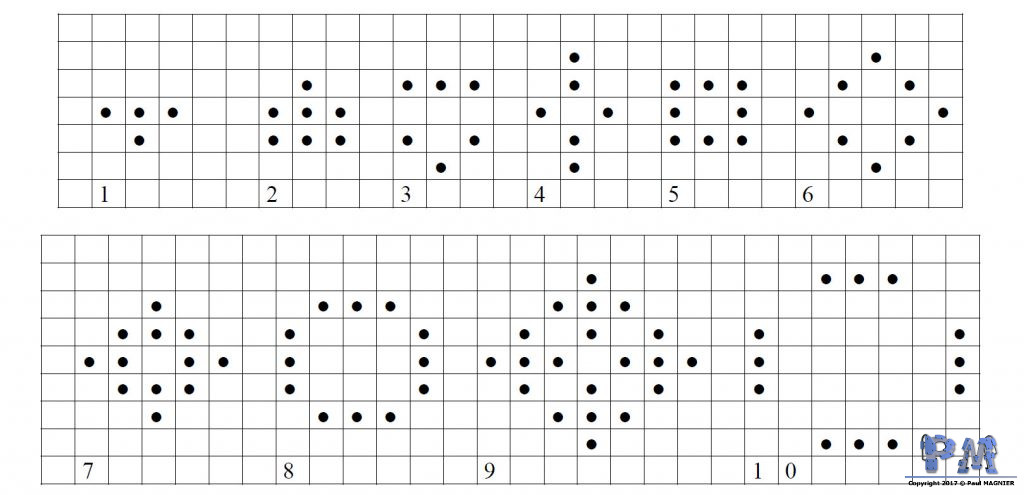
Exemple d’évolution

Un exemple de développement pour une grille est le suivant :

L’algorithme peut entrainer l’apparition de structure particulière découlant des règles particulières qui le régissent.

3 types de structures principales peuvent être différenciées:

• Les structures stables sont des ensembles de cellules ayant stoppé toute évolution. Elles sont dans un état stationnaire et n’évoluent plus tant qu’aucun élément perturbateur n’apparaît dans leur voisinage.
• Les oscillateurs se transforment de manière cyclique, en revêtant plusieurs formes différentes avant de retrouver leur état initial.
• Les vaisseaux sont des structures capables, après un certain nombre de générations, de produire une copie d’elles-mêmes, mais décalée dans l’univers du jeu.